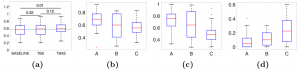
Moving beyond simply assessing classification and reconstruction performance, experts categorized the syndromes into three classes of syndromes, of which two include syndromes that are phenotypically distinctive (A and B) and the third class of syndromes that is not necessarily phenotypically distinctive (C). We assessed whether the latent space conforms to expectations based on prior knowledge from clinical genetics by testing if phenotypically distinctive groups are positioned relatively distantly from, and with minimal overlap, to controls. Further, we tested for expected overlap among four RASopathies, an etiologically related group of disorders caused by mutations in genes encoding the RAS/MAPK pathway.
Classification and Reconstruction The average group sensitivities of the models that we trained are shown by boxplots in Fig. 2a. Differences in performance among the models were compared statistically with pairwise comparisons using a paired two-tailed Wilcoxon signed-rank test. The performance of the TBAE is significantly higher than the baseline (pvalue <0.05). The median of the TBE and TBAE is not significantly different, however, the pvalue=0.12 supports suggestive improvement. Also, the lower quartile has improved by TBAE which indicates that learning facial similarity alongside group-dissimilarity by attaching a decoder improves the results for some groups. The average reconstruction error for syndromic and control individuals is shown in Fig. 3a. The average error per vertex is less than 1 mm. Nevertheless, the heat maps indicate that regions around the mouth, nose, and eyes show relatively higher errors. This is more pronounced in syndrome groups compared to the controls. The lips and mouth regions are sensitive to expression variation, introducing extra complexity for the model to learn. The low reconstruction error of control faces shown in Fig. 3a supports the hypothesis that normal facial variation can be presented from the facial variation within the syndrome groups. To assess the visual plausibility and smoothness of the reconstructions from the metric space, some of the reconstructions of the average test set projections are shown in Fig. A.1 in the supplementary material.

Metric Space Evaluation Fig. 2b compares the distributions of syndrome group sensitivities among syndromes assigned to the phenotypically distinctive categories A and B and the less distinctive category C. Those syndromes in categories A and B have higher median sensitivities than those in category C, with B showing slightly lower sensitivities than A. Fig. 2c and 2d compare the distributions of the proximity and overlap statistics respectively for syndromes within each category. These reflect the proximity and overlap of each syndrome to the controls. In general, as predicted, syndromes in categories A and B are more distant from and overlap less with, controls than those in category C. Graphically, this is shown in the t-SNE visualization (Fig. 3b) which shows syndromes in category A and B are more distant from controls than category C.

Noonan, Costello, Cardiofaciocutaneous syndrome, and Neurofibromatosis Type I (NF1) are members of an etiologically related group of disorders, collectively known as the RASopathies [11]. These syndromes are all caused by the overactivation of the RASMAPK pathway and are known to show considerable phenotypic similarity and overlap. Within the latent space these had a proximity statistic over 97.4%, and an overlap statistic higher than ¿99.9% of random samples of four syndrome groups (the p-values of the hypothesis tests of the closeness and overlap statistics were .036 and <.001 respectively). These results indicate these syndromes are very close together with high overlap in the latent space, as would be expected from their known genetic and phenotypic relationships. The t-SNE plot in Fig. 3c shows these disorders grouped in the lower corner and NF1 is the most dispersed, overlapping considerably with controls. This is also consistent with clinical expectations as NF1 is assigned to category C and is not usually considered to have a distinctive facial phenotype.

The goal of this study was to go beyond classification for aiding in syndrome diagnosis and therefore, to invest in learning a well-structured metric space that can help the study of phenotype-genotype relationships. Future directions include: First, comparing the classification results of our approach with those of Face2gene [4], software often used in clinical workups to assess 2D facial im- ages for syndrome diagnosis. In this context, it is a major challenge to obtain equivalent 2D and 3D datasets for direct comparison. Second, this work might be extended by taking a part-based approach, in which the variation of localized facial segments could be learned both in isolation and in combination. Finally, the adaption of this metric space into clinics will require further validation towards targeted sequencing and genetic variant analysis and classification.